Calculate Statistical Significance: Importance & Method
Did you know that statistical significance is a crucial concept in data analysis and research? Whether you’re conducting a scientific study, running marketing experiments, or making data-driven decisions, understanding statistical significance is essential for drawing accurate conclusions from your data. In this article, we’ll explore the importance of statistical significance and discuss the methods used to calculate it.
Why is Statistical Significance Important?
Statistical significance helps researchers determine whether the results of a study or experiment are due to chance or if they actually represent a meaningful difference or relationship. It allows us to make confident statements about the data and draw reliable conclusions. Here are a few reasons why statistical significance is important:
- Validating Hypotheses: Statistical significance helps researchers determine whether their hypotheses are supported by the data. It allows them to draw meaningful conclusions and make informed decisions based on their findings.
- Generalizability: Statistical significance helps us determine if the results of a study or experiment can be generalized to a larger population. If the results are statistically significant, we can confidently apply them to the broader population.
- Reducing Errors: Statistical significance helps minimize the risk of making Type I and Type II errors. Type I errors occur when we mistakenly reject a true null hypothesis, while Type II errors occur when we fail to reject a false null hypothesis. Calculating statistical significance helps us find the right balance between these two types of errors.
Methods to Calculate Statistical Significance
There are several methods available to calculate statistical significance, depending on the type of data and the research question at hand. Here are some commonly used methods:
T-Test
The t-test is a statistical method used to compare the means of two groups and determine if there is a significant difference between them. It is commonly used in hypothesis testing and can be applied to both parametric and non-parametric data.
Chi-Square Test
The chi-square test is used to determine if there is a significant association between two categorical variables. It compares the observed frequencies with the expected frequencies to assess the independence of the variables.
Analysis of Variance (ANOVA)
ANOVA is a statistical method used to compare the means of three or more groups and determine if there is a significant difference between them. It is commonly used when dealing with multiple treatments or factors.
Correlation Analysis
Correlation analysis is used to measure the strength and direction of the linear relationship between two continuous variables. It determines if there is a significant correlation between the variables and helps assess the predictive power of one variable on another.
Regression Analysis
Regression analysis is used to model the relationship between a dependent variable and one or more independent variables. It helps determine if there is a significant association between the variables and allows for prediction and inference.
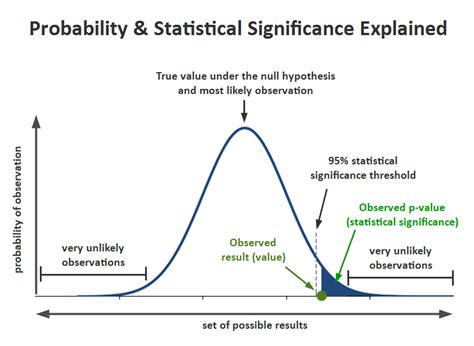
Significance Testing
Significance testing is a general framework used to determine if the observed results are statistically significant. It involves calculating p-values, which represent the probability of obtaining the observed results by chance alone. If the p-value is below a predetermined significance level (usually 0.05), the results are considered statistically significant.
Conclusion
Statistical significance is a vital concept in data analysis and research. It allows us to make confident conclusions, validate hypotheses, and minimize errors. By employing various statistical methods such as t-tests, chi-square tests, ANOVA, correlation analysis, regression analysis, and significance testing, we can accurately calculate statistical significance and draw meaningful insights from our data.
Frequently Asked Questions
- What is the significance level?
- What does a p-value less than 0.05 mean?
- Can statistical significance guarantee practical significance?
- What sample size is needed for statistical significance?
- Is statistical significance the same as clinical significance?
The significance level, also known as alpha, is the predetermined threshold below which the p-value must fall to consider the results statistically significant. It is typically set at 0.05.
A p-value less than 0.05 means that there is a less than 5% probability of obtaining the observed results by chance alone. This indicates that the results are statistically significant.
No, statistical significance does not guarantee practical significance. While statistical significance indicates a meaningful difference or relationship in the data, practical significance refers to the real-world importance or impact of the findings.
The sample size needed for statistical significance depends on various factors such as the desired level of precision, effect size, and variability of the data. Power analysis can help determine the appropriate sample size for a study.
No, statistical significance is not the same as clinical significance. Clinical significance refers to the practical importance or relevance of the findings in a clinical context, while statistical significance focuses on the probability of obtaining the observed results by chance.
Sarah Thompson
Sarah Thompson is a career development expert with a passion for helping individuals achieve their professional goals. With over a decade of experience in the field, Sarah specializes in providing practical advice and guidance on job search strategies, cover letters, resumes, and interview techniques. She believes in empowering job seekers with the knowledge and tools necessary to navigate the competitive job market successfully.